Table of contents
This is a series continuation of Introduction to Algorithm: Linear Search versus binary search. Where we also discussed sorted and unsorted searches. You have to go through the first material before jumping on this as it is a continuation and you can only understand this after going through the first.
Here is the link to the first part of this series.
https://michelle-buchi.hashnode.dev/introduction-to-algorithm-linear-search-vs-binary-search
Bubble sort:
An algorithm is used to sort a set of elements. The idea is to move higher-value elements to the right and lower-value elements to the left.
How it works
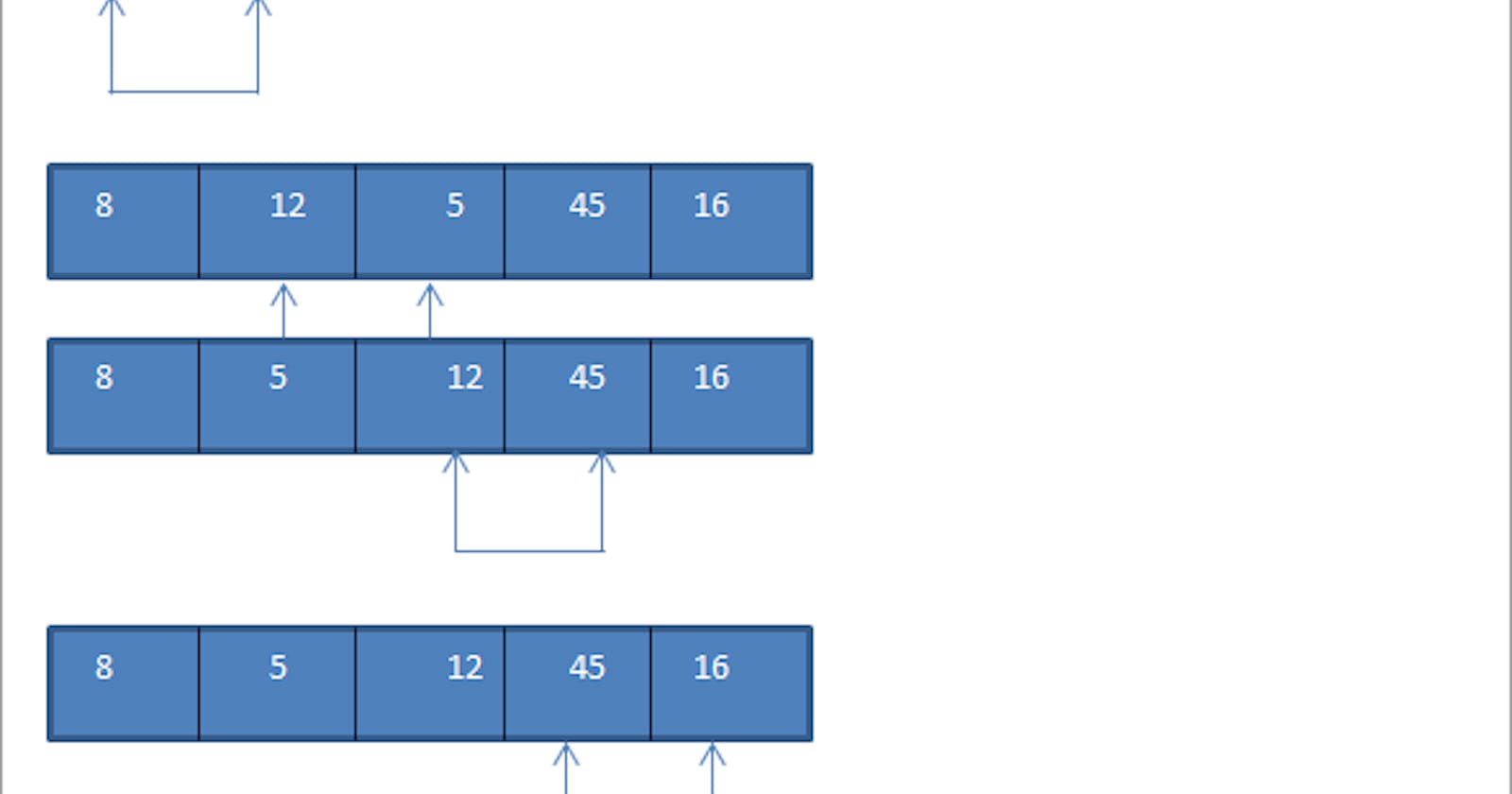
Set the swap counter to a non-zero value. Repeat until the swap counter is 0: Reset the swap counter to 0. Look at each adjacent pair If two adjacent elements are not in order, swap them and add one to the swap.
Eg
Let swapCounter = 2;
Let arr=[9,4,5,1,8,7,2]
First, we need to reset the swap counter to zero then we look at each adjacent pair.
To reset, swapCounter now equals 0. swapCounter == 0;
The first pair is 9 and 4
[9,4,5,1,8,7,2]
They are out of order. We need to swap them. Then swapCounter++; swapCounter = 1; Now, we have
[4, 9,5,1,8,7,2]
The next pair is 9 and 5. They are also out of order.
[4, 9,5,1,8,7,2]
We need to swap them swapCounter++; swapCounter == 2; Now we have
[4,5, 9,1,8,7,2]
The next pair is 9 and 1. They are out of order [4,5, 9,1,8,7,2] so we need to swap them. swapCounter++; swapCounter == 3; Now we have
[4,5,1, 9,8,7,2]
The next pair is 9 and 8. They are not out of order
[4,5,1, 9,8,7,2]
so we swap them swapCounter++; swapCounter == 4;
The next pair is 9 and 7. They are out of order. so we swap them.
[4,5,1,8, 9,7,2]
The next pair is 8 and 7. They are out of order
[4,5,1,8,7 9,2]
so we swap them swapCounter++ swapCounter = 5; Now we have [4,5,9,1,7, 8,2]
The next pair is 8 and 2. They are out of order
[4,5,1,8,7, 9,2]
so we swap them swapCounter++; swapCounter = 6; Now we have
[4,5,1,8,7,2, 9]
We start from the top again with this new array.
- The idea is to repeat this procedure until the swapCounter == 0;
So we reset the swapCounter again swapCounter = 0;
Arr = [4,5,9,1,7,2,8]
The first pair here is 4 and 5. They are inorder
[4,5, 9,1,7,2,8]
so we don’t swap them. Hence, we don’t increase the swapCounter. swapCounter == 0
The next one is 5 and 9. They are in order
[4,5,9, 1,7,2,8]
so we don’t swap them Hence, we don’t increase the swapCounter. swapCounter == 0.
The next one is 9 and 1. They are out of order
[4,5,9,1,7,2,8]
so we swap them.
[4,5,1, 9,7,2,8]
swapCounter++; swapCounter = 1; Now we have
[4,5,1, 9,7,2,8]
The next pair is 9 and 7. They are out of order
[4,5,1, 9,7,2,8]
so we swap them
[4,5,1,7 9,2,8]
swapCounter++; swapCounter = 2; Now we have
[4,5,1,7, 9,2,8]
The next pair is 9 and 2. They are out of order
[4,5,1, 9,2,8]
so we swap them.
[4,5,1,2 9,8]
swapCounter++; swapCounter == 3; Now we have
[4,5,1,7,2, 9,8]
The next pair is 9 and 8. They are out of order
[4,5,1,2 9,8]
so we swap them.
[4,5,1,2, 9,8]
swapCounter++; swapCounter == 4; Now we have
[4,5,1,7,2,8,9]
Now we have
[4,5,1,7,2,8,9]
So we have to start again since we got to the end of the swap. Reset swapCounter swapCounter == 0;
The first pair here is 4 and 5. It is in order.
[4,5, 1,7,2,8,9]
swapCounter == 0; The next pair is 5 and 1. It is out of order
[4,5, 1,7,2,8,9]
we need to swap them swapCounter++; swapCounter == 1; Now we have
[4,1,5, 7,2,8,9]
The next pair is 5 and 7. It is in order
[4,1,5,7, 2,8,9]
swapCounter == 1;
The next pair is 7 and 2. it is out of order
[4,1,5,7, 2,8,9]
so we swap swapCounter++; swapCounter == 2; Now we have
[4,1,5,2,7, 8,9]
The next pair is 7 and 8. They are in order
[4,1,5,2,7,8, 9]
swapCounter == 2;
The next pair is 8 and 9. They are in order.
[4,1,5,2,7,8,9]
swapCounter == 2;
We start from the beginning again Reset the swapCounter swapCounter == 0;
The first pair is out of order
[4,1,5,2,7,8,9]
so we swap them swapCounter++; swapCounter == 1; Now we have
[1,4, 5,2,7,8,9]
The next pair is 4 and 5. They are in order
[1,4,5, 2,7,8,9]
swapCounter == 1;
The next pair is 5 and 2. They are out of order
[1,4,5, 2,7,8,9]
so we swap them
[1,4,5, 2,7,8,9]
swapCounter++; swapCounter == 2; Now we have
[1,4,2,5, 7,8,9]
The next pair is 5 and 7. They are in order.
[1,4,2,5,7, 8,9]
swapCounter == 2;
The next pair is 7 and 8. They are in order.
[1,4,2,5,7,8, 9]
swapCounter == 2;
The next pair is 8 and 9. They are in order.
[1,4,2,5,7,8, 9]
swapCounter == 2;
We start from the beginning again Reset swapCounter swapCounter == 0;
arr = [1,4,2,5,7,8,9]
The first pair is 1 and 4. They are in order
[1,4, 2,5,7,8,9]
swapCounter == 0;
The next pair is 4 and 2. They are out of order
[1,4, 2,5,7,8,9]
so swap them. swapCounter++; swapCounter == 1; Now we have
[1,2,4, 5,7,8,9]
The next pair is 4 and 5. They are in order
[1,2,4,5, 7,8,9]
swapCounter == 1;
The next pair is 5 and 7. They are in order
[1,2,4,5,7, 8,9]
swapCounter == 1;
The next pair is 7 and 8. They are in order
[1,2,4,5,7,8, 9]
swapCounter == 1;
The next pair is 8 and 9. They are in order.
[1,2,4,5,7,8,9]
swapCounter == 1;
We start from the beginning
Reset swapCounter = 0;
The first pair is 1 and 2. They are in order. The next pair is 2 and 4. They are in order. The next pair is 4 and 5. They are in order. The next pair is 5 and 7. They are in order The next pair is 7 and 8. They are in order. The next pair is 8 and 9. They are in order
So we have
[1,2,4,5,7,8,9]
swapCounter = 0;
Here, we can declare the entire array sorted since swapCounter = 0;
Worst-case scenario: The array is in reverse order, we have to bubble each of the n elements all the way across the array, and since we can only fully bubble one element into position per pass, we must do this n times. The formula is O(n square) since you have to go through all the elements
Best-case scenario: The array is already perfectly sorted and we make no swaps on the first pass. The formular is omega(n).
Selection Sort
It is an algorithm that sorts a set of elements. The idea is to find the smallest unsorted element and add it to the sorted list.
To achieve this: Repeat the process of finding the smallest element in the array Search the unsorted part of the data to find the smallest value Swap the smallest found value with the first element of the unsorted part.
Let arr = [9,4,6,3,5,7,1,8]
We search through the array to find the smallest value smallestValue = 1;
Next, swap that value with the first element of the unsorted part So we swap 9 and 1 We now have
[1, 4,6,3,5,7,9,8]
We repeat the process again for the unsorted part
The smallest value of the unsorted array is 3
[1, 4,6,3,5,7,9,8]
Swap it with the first element of the unsorted part. So we swap 4 and 3 Now, we have
[1,3, 6,4,5,7,9,8]
Next, we repeat again
smallestValue of the unsorted part = 4
[1,3, 6,4,5,7,9,8]
Swap it with the first element of the unsorted part We swap 6 and 4 Now we have
[1,3,4, 6,5,7,9,8]
Next, we repeat again the smallestValue of the unsorted array = 5
[1,3,4, 6,5,7,9,8]
Swap 6 and 5 Now we have
[1,3,4,5, 6,7,9,8]
Next, we repeat again
The smallestValue of the unsorted part = 6
[1,3,4,5, 6,7,9,8]
Which happens to be the first element of the unsorted part
[1,3,4,5,6, 7,9,8]
Next the smallestValue = 7;
It is also the first element of the unsorted part
[1,3,4,5,6, 7,9,8]
it becomes
[1,3,4,5,6,7, 9,8]
Next, the smallestValue = 8;
[1,3,4,5,6,7, 9,8]
Swap 9 and 8 Now we have
[1,3,4,5,6,7,8, 9]
Next, the only value left is 9
[1,3,4,5,6,7,8, 9]
We move it to the sorted part.
[1,3,4,5,6,7,8,9]
Worst-case scenario: We have to loop over all the elements of the array to find the smallest unsorted element and we must repeat this process n times since only one element gets sorted on each pass. It is represented as O(n square).
Best-case scenario: there is no way to guarantee the array is sorted until we go through the same process for all the elements. It is represented as omega(n square).
Follow me on Twitter Handle: https://twitter.com/mchelleOkonicha
Follow me on LinkedIn Handle: https://www.linkedin.com/in/buchi-michelle-okonicha-0a3b2b194/